企业研发之独轮车开发
12月14日我们坐着大巴一路辗转来到青岛,但路途的劳累随着我们进入公司一扫而空。洁净的地面,炫酷的操作台,井然有序的工作环境,无不让我们为止惊叹,一个个都摩拳擦掌,跃跃欲试。随后公司负责向我们简要介绍了公司相关信息以及各组别的科研任务,非常幸运,我和两位同学被分到了独轮车的研究项目。

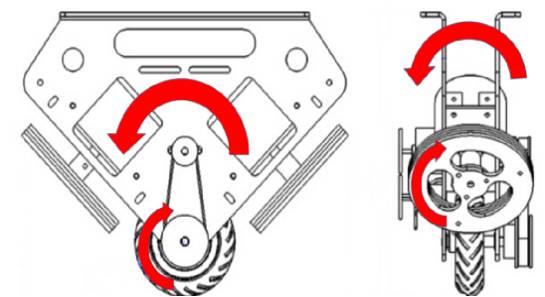
什么是独轮车呢?独轮车的样子即如右图所示,整个车模由两个飞轮来控制左右平衡和方向旋转,由行进电机保持前后平衡和前进后退,这一点和传统的两轮平衡车控制思路是一致的,车模结构也比较简单。首先有了对独轮车大致的认识和一定的技术猜想,我们打算分块进行研究与开发,我们主要分为了硬件和软件两大部分,其中硬件的开发周期长,所需的知识储备要求较高,于是在短短的一个多月的实习中,我们将工作重心放在了软件程序的调试。
即使是程序编写也有大讲究,独轮车能够保持平衡的在于通过程序精准控制飞轮和行进电机的旋转,根据牛顿第三运动定律:相互作用的两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在同一条直线上。举个简单的例子,飞轮顺时针旋转时,车身将受到围绕旋转轴的逆时针方向的力,并且力的大小和驱动飞轮的力大小一致,此时理论上车身应围绕旋转轴逆时针旋转,但由于小车与地面接触,摩擦力的存在导致本应围绕飞轮旋转轴而旋转的车身变成了围绕小车底部旋转,这恰巧是我们所需要的,能够通过飞轮控制车模进行左右倾斜的操作,只要控制程序足够精细,那么就可以保持左右平衡。同理,通过行进电机亦可完成前后平衡的控制。
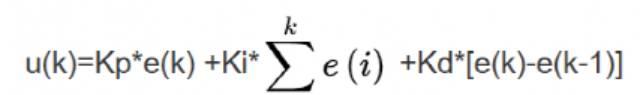
经过物理分析,我们最终确定使用PID算法作为控制算法,PID分为三部分:Proportional(比例)、Integral(积分)、Differential(微分)。PID算法最根本的目的就是使实际值无限接近于目标值,当实际值与目标值不相等时,将其做差后得到的差值我们称为误差,而PID所有的计算也是基于误差进行计算的。其中,P是比例量,是将误差值直接乘以一个系数,有了比例量的加持,可以让误差快速缩小,让实际值快速接近目标值。当实际值在目标值附近时,因为比例量的特性,实际值会在目标值附近一直抖动,此时就需要引入微分量。D是微分量,简单来说就是本次的误差与上一次的误差之间的差值再乘以一个系数,它可以抑制一部分的比例量,当实际值因为比例量的计算而在目标值附近反复横跳时,微分量就可以将其抑制住,使其保持稳定。稳定后实际值与目标值之间还存在较小的误差,这是由于微分量和比例量抵消后的结果,此时就需要引入积分量来将这部分的误差消除掉。I量是积分量,积分的意思就是将误差一直累加起来再乘以一个系数,上面简述了PD计算之后会出现一个稳定的误差值,虽然这个误差比较小,但我们将这个误差一直累加起来就很大了,最后肯定可以将这个误差消除掉。当然,为了防止积分量过大,我们一般会对其进行限幅。和小伙伴们讨论完了基本算法后就开始如火如荼的进行程序编写和参数调试了,期间我们遇到了无数的困难,诸如程序烧录错误,多核链接异变,串口数据混乱,实际效果与理想状态相距甚远等等,在与这些问题的交手中,我们也逐渐了解到信息检索能力和寻找对标能力的重要性,在直面这些困难后,我们也终于让我们的小车平衡起来,现在回头看,真可谓“轻舟已过万重山”。所有的困难都逐渐解决,我们也逐步摸索出了自己的企研之路。


http://www.dxsbao.com/shijian/548693.html 点此复制本页地址





